Publications

2024

1. 

   Neural Interactive Proofs

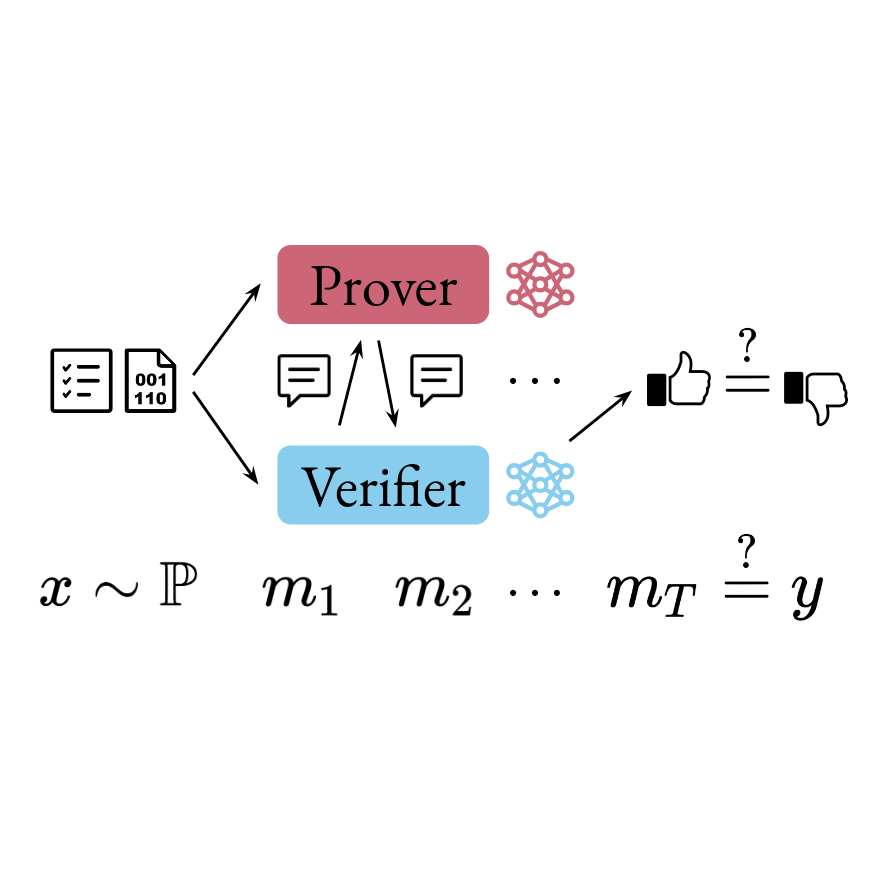   Lewis Hammond, and Sam Adam-Day

   2024

   Preprint

   Abs arXiv Bib

   We consider the problem of how a trusted, but computationally bounded agent (a ’verifier’) can learn to interact with one or more powerful but untrusted agents (’provers’) in order to solve a given task without being misled. More specifically, we study the case in which agents are represented using neural networks and refer to solutions of this problem as neural interactive proofs. First we introduce a unifying framework based on prover-verifier games (Anil et al., 2021), which generalises previously proposed interaction ’protocols’. We then describe several new protocols for generating neural interactive proofs, and provide a (theoretical) comparison of both new and existing approaches. In so doing, we aim to create a foundation for future work on neural interactive proofs and their application in building safer AI systems.

   @misc{hammond-adam-day-2024-nip,
     author = {Hammond, Lewis and Adam-Day, Sam},
     title = {Neural Interactive Proofs},
     year = {2024},
     note = {Preprint},
     howpublished = {Preprint},
     booktitle = {Next Generation of AI Safety Workshop, ICML '24},
     eprint = {2412.08897},
     archiveprefix = {arXiv},
     primaryclass = {cs.AI},
   }

2. 

   Almost Surely Asymptotically Constant Graph Neural Networks

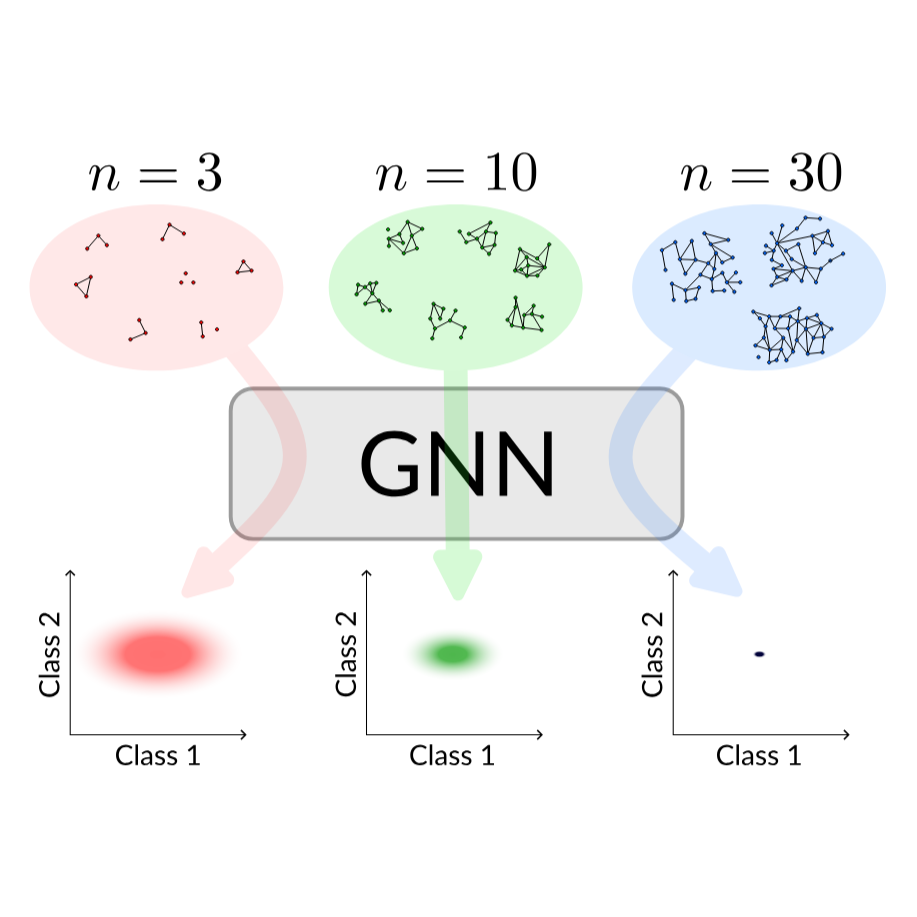   Sam Adam-Day, Michael Benedikt, İsmail İlkan Ceylan, and Ben Finkelshtein

   In Proceedings of the 38th Annual Conference on Neural Information Processing Systems (NeurIPS), 2024

   Abs arXiv Bib HTML

   Graph neural networks (GNNs) are the predominant architectures for a variety of learning tasks on graphs. We present a new angle on the expressive power of GNNs by studying how the predictions of a GNN probabilistic classifier evolve as we apply it on larger graphs drawn from some random graph model. We show that the output converges to a constant function, which upper-bounds what these classifiers can express uniformly. This convergence phenomenon applies to a very wide class of GNNs, including state of the art models, with aggregates including mean and the attention-based mechanism of graph transformers. Our results apply to a broad class of random graph models, including the (sparse) Erdős-Rényi model and the stochastic block model. We empirically validate these findings, observing that the convergence phenomenon already manifests itself on graphs of relatively modest size.

   @inproceedings{adam-day-et-al-2024-aas-constant,
     author = {Adam-Day, Sam and Benedikt, Michael and Ceylan, İsmail İlkan and Finkelshtein, Ben},
     booktitle = {Proceedings of the 38th Annual Conference on Neural Information Processing Systems (NeurIPS)},
     title = {Almost Surely Asymptotically Constant Graph Neural Networks},
     year = {2024},
     eprint = {2403.03880},
     archiveprefix = {arXiv},
     primaryclass = {cs.LG},
     url = {https://openreview.net/forum?id=Dn68qdfTry},
   }

2023

1. 

   Zero-One Laws of Graph Neural Networks

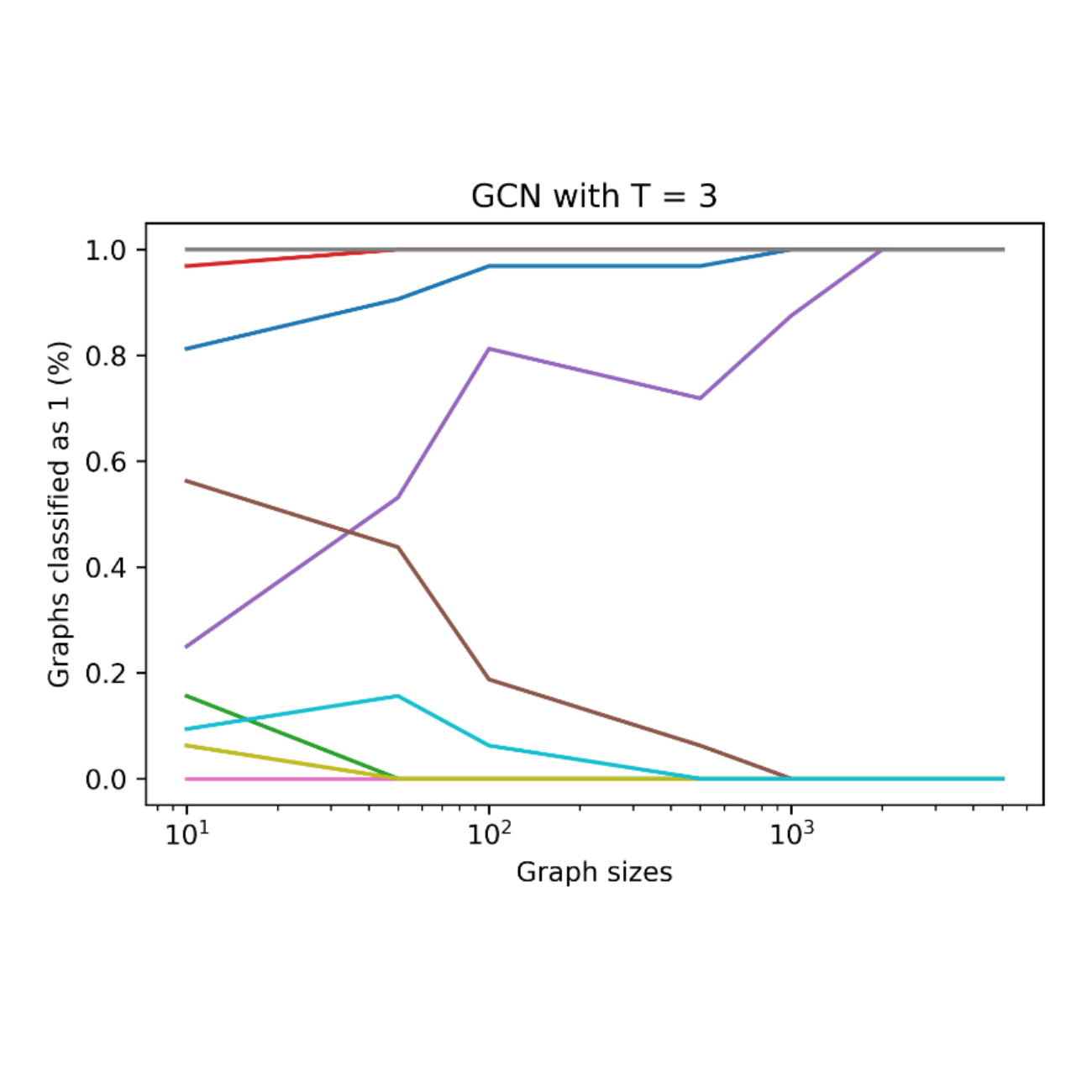   Sam Adam-Day, Theodor Mihai Iliant, and İsmail İlkan Ceylan

   In Proceedings of the 37th Annual Conference on Neural Information Processing Systems (NeurIPS), 2023

   Abs arXiv Bib HTML

   Graph neural networks (GNNs) are de facto standard deep learning architectures for machine learning on graphs. This has led to a large body of work analyzing the capabilities and limitations of these models, particularly pertaining to their representation and extrapolation capacity. We offer a novel theoretical perspective on the representation and extrapolation capacity of GNNs, by answering the question: how do GNNs behave as the number of graph nodes become very large? Under mild assumptions, we show that when we draw graphs of increasing size from the Erdős-Rényi model, the probability that such graphs are mapped to a particular output by a class of GNN classifiers tends to either zero or to one. This class includes the popular graph convolutional network architecture. The result establishes ’zero-one laws’ for these GNNs, and analogously to other convergence laws, entails theoretical limitations on their capacity. We empirically verify our results, observing that the theoretical asymptotic limits are evident already on relatively small graphs.

   @inproceedings{adam-day-et-al-2023-zero-one-laws,
     author = {Adam-Day, Sam and Iliant, Theodor Mihai and Ceylan, İsmail İlkan},
     booktitle = {Proceedings of the 37th Annual Conference on Neural Information Processing Systems (NeurIPS)},
     title = {Zero-One Laws of Graph Neural Networks},
     year = {2023},
     eprint = {2301.13060},
     archiveprefix = {arXiv},
     primaryclass = {cs.LG},
     url = {https://openreview.net/forum?id=DGmxTUCHYs},
   }

2. 

   Branchwise-real trees and bisimulations of potentialist systems

   Sam Adam-Day

   University of Oxford, 2023

   PhD Thesis

   Abs Bib HTML

   This thesis concerns two topics. The first treats R-trees, which are a certain kind of metric space tree in which every point can be branching. Favre and Jonsson posed the following problem in 2004: can the class of partial orders underlying R-trees be characterised by the fact that every branch is order-isomorphic to a real interval? I first answer this question in the negative, then go on to establish a connection between these trees and traditional set-theoretic trees. This connection is then put to work, answering refinements of Favre and Jonsson’s question, yielding several independence results. I next move on to consider the existence of examples of these partial orders without non-trivial automorphisms. I provide constructions of these subject to increasingly strong uniformity conditions. While these constructions all take place in ZFC, they have a strong forcing flavour. The second topic deals with bisimulations of potentialist systems, which are first-order Kripke models based on embeddings. Given a first-order theory T we can impose a potentialist structure on the class of models of T by taking either all embeddings or all substructure inclusions between models. I show that these two systems are always bisimilar. Next, by connecting with a generalisation of the Ehrenfeucht-Fraïsé game, I show the equivalence of the existence of a bisimulation with elementary equivalence with respect to an infinitary language. Finally, I turn to the question of when a class-sized potentialist system is bisimilar to a set-sized one, providing two different sufficient conditions.

   @phdthesis{adam-day2023-phd-thesis,
     publisher = {University of Oxford},
     school = {University of Oxford},
     title = {Branchwise-real trees and bisimulations of potentialist systems},
     author = {Adam-Day, Sam},
     year = {2023},
     url = {https://ora.ox.ac.uk/objects/uuid:72dd8acb-10bb-47f5-8a44-cb56e7a7e5a7},
     note = {PhD Thesis},
   }

3. 

   The Intermediate Logic of Convex Polyhedra

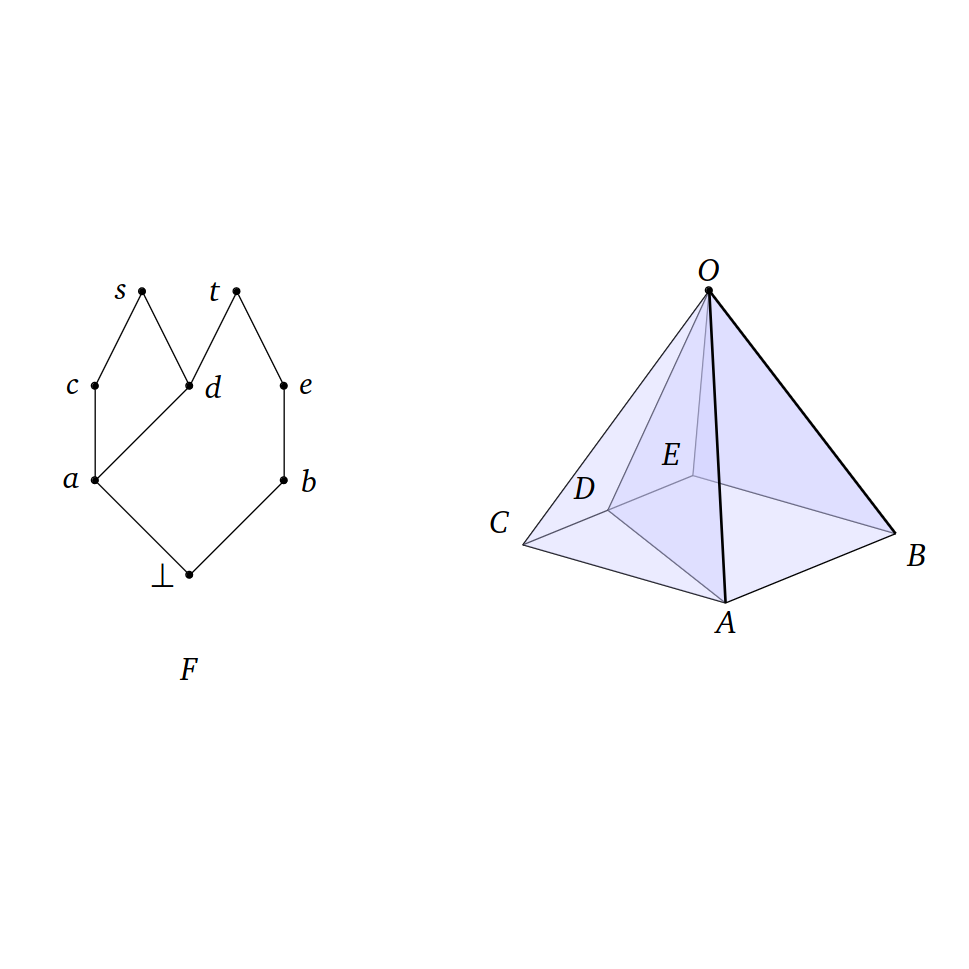   Sam Adam-Day, Nick Bezhanishvili, David Gabelaia, and Vincenzo Marra

   2023

   Preprint

   Abs arXiv Bib

   We investigate a recent semantics for intermediate (and modal) logics in terms of polyhedra. The main result is a finite axiomatisation of the intermediate logic of the class of all polytopes – i.e., compact convex polyhedra – denoted PL. This logic is defined in terms of the Jankov-Fine formulas of two simple frames. Soundness of this axiomatisation requires extracting the geometric constraints imposed on polyhedra by the two formulas, and then using substantial classical results from polyhedral geometry to show that convex polyhedra satisfy those constraints. To establish completeness of the axiomatisation, we first define the notion of the geometric realisation of a frame into a polyhedron. We then show that any PL frame is a p-morphic image of one which has a special form: it is a ’sawed tree’. Any sawed tree has a geometric realisation into a convex polyhedron, which completes the proof.

   @misc{adam-day-et-al-2023-convex-polyhedra,
     author = {Adam-Day, Sam and Bezhanishvili, Nick and Gabelaia, David and Marra, Vincenzo},
     note = {Preprint},
     howpublished = {Preprint},
     title = {The Intermediate Logic of Convex Polyhedra},
     year = {2023},
     eprint = {2307.16600},
     archiveprefix = {arXiv},
     primaryclass = {math.LO},
   }

2022

1. 

   On the continuous gradability of the cut-point orders of R-trees

   Sam Adam-Day

   Topology and its Applications, 2022

   Abs arXiv Bib HTML

   An \(\mathbb R\)-tree is a certain kind of metric space tree in which every point can be branching. Favre and Jonsson posed the following problem in 2004: can the class of orders underlying \(\mathbb R\)-trees be characterised by the fact that every branch is order-isomorphic to a real interval? In the first part, I answer this question in the negative: there is a ’branchwise-real tree order’ which is not ‘continuously gradable’. In the second part, I show that a branchwise-real tree order is continuously gradable if and only if every well-stratified subtree is \(\mathbb R\)-gradable. This link with set theory is put to work in the third part answering refinements of the main question, yielding several independence results. For example, when \(κ≥\mathfrak c\), there is a branchwise-real tree order which is not continuously gradable, and which satisfies a property corresponding to \(κ\)-separability. Conversely, under Martin’s Axiom at \(κ\)such a tree does not exist.

   @article{adam-day-2022-continuous-gradability,
     author = {Adam-Day, Sam},
     journal = {Topology and its Applications},
     title = {On the continuous gradability of the cut-point orders of R-trees},
     volume = {306},
     year = {2022},
     doi = {https://doi.org/10.1016/j.topol.2021.107937},
     url = {https://www.sciencedirect.com/science/article/pii/S0166864121003540},
     keywords = {R-tree, Branchwise-real tree order, Continuous grading, Road space, Suslin tree, Martin's Axiom, Independence result, Separable, Countable chain condition},
     eprint = {2107.14718},
     archiveprefix = {arXiv},
     primaryclass = {math.LO},
   }

2. 

   Uniform, rigid branchwise-real trees

   Sam Adam-Day

   2022

   Preprint accepted by the Israel Journal of Mathematics

   Abs arXiv Bib

   A branchwise-real tree order is a partial order tree in which every branch is isomorphic to a real interval. I give constructions of such trees which are both rigid (i.e. without non-trivial order-automorphisms) and uniform (in two different senses). Specifically, I show that there is a rigid branchwise-real tree order in which every branching point has the same degree, one in which every point is branching and of the same degree, and finally one in which every point is branching of the same degree and which admits no order-preserving function into the reals. Trees are grown iteratively in stages, and a key technique is the construction (in ZFC) of a family of colourings of \((0,∞)\)which is ’sufficiently generic’, using these colourings to determine how to proceed with the construction.

   @misc{adam-day-2022-rigid-trees,
     author = {Adam-Day, Sam},
     note = {Preprint accepted by the Israel Journal of Mathematics},
     howpublished = {Preprint accepted by the Israel Journal of Mathematics},
     title = {Uniform, rigid branchwise-real trees},
     year = {2022},
     eprint = {2206.15344},
     archiveprefix = {arXiv},
     primaryclass = {math.LO},
   }

3. 

   Bisimulations of potentialist systems

   Sam Adam-Day

   2022

   Preprint submitted to the Journal of Symbolic Logic

   Abs arXiv Bib

   A potentialist system is a first-order Kripke model based on embeddings. I define the notion of bisimulation for these systems, and provide a number of examples. Given a first-order theory \(T\), the system Mod(\(T\)) consists of all models of \(T\). We can then take either all embeddings, or all substructure inclusions, between these models. I show that these two ways of defining Mod(\(T\)) are bitotally bisimilar. Next, I relate the notion of bisimulation to a generalisation of the Ehrenfeucht-Fraïsé game, and use this to show the equivalence of the existence of a bisimulation with elementary equivalence with respect to an infinitary language. Finally, I consider the question of when a potentialist system is bitotally bisimilar to a system containing set-many models, providing too different sufficient conditions.

   @misc{adam-day-2022-bisimulations,
     author = {Adam-Day, Sam},
     note = {Preprint submitted to the Journal of Symbolic Logic},
     howpublished = {Preprint submitted to the Journal of Symbolic Logic},
     title = {Bisimulations of potentialist systems},
     year = {2022},
     eprint = {2206.10359},
     archiveprefix = {arXiv},
     primaryclass = {math.LO},
   }

4. 

   Polyhedral completeness of intermediate logics: the Nerve Criterion

   Sam Adam-Day, Nick Bezhanishvili, David Gabelaia, and Vincenzo Marra

   The Journal of Symbolic Logic, 2022

   Abs arXiv Bib HTML

   We investigate a recently-devised polyhedral semantics for intermediate logics, in which formulas are interpreted in n-dimensional polyhedra. An intermediate logic is polyhedrally complete if it is complete with respect to some class of polyhedra. The first main result of this paper is a necessary and sufficient condition for the polyhedral-completeness of a logic. This condition, which we call the Nerve Criterion, is expressed in terms of Alexandrov’s notion of the nerve of a poset. It affords a purely combinatorial characterisation of polyhedrally-complete logics. Using the Nerve Criterion we show, easily, that there are continuum many intermediate logics that are not polyhedrally-complete but which have the finite model property. We also provide, at considerable combinatorial labour, a countably infinite class of logics axiomatised by the Jankov-Fine formulas of ’starlike trees’ all of which are polyhedrally-complete. The polyhedral completeness theorem for these ’starlike logics’ is the second main result of this paper.

   @article{adam-day-et-al-2022-poly-completeness,
     author = {Adam-Day, Sam and Bezhanishvili, Nick and Gabelaia, David and Marra, Vincenzo},
     journal = {The Journal of Symbolic Logic},
     publisher = {Cambridge University Press},
     title = {Polyhedral completeness of intermediate logics: the Nerve Criterion},
     year = {2022},
     doi = {10.1017/jsl.2022.76},
     pages = {1–41},
     url = {https://doi.org/10.1017/jsl.2022.76},
     eprint = {2112.07518},
     archiveprefix = {arXiv},
     primaryclass = {math.LO},
   }

2020

1. 

   Non-mathematical Content by Mathematical Means

   Sam Adam-Day

   2020

   Abs Bib HTML PDF

   In this paper, I consider the use of mathematical results in philosophical arguments arriving at conclusions with non-mathematical content, with the view that in general such usage requires additional justification. As a cautionary example, I examine Kreisel’s arguments that the Continuum Hypothesis is determined by the axioms of Zermelo-Fraenkel set theory, and interpret Weston’s 1976 reply as showing that Kreisel fails to provide sufficient justification for the use of his main technical result. If we take the perspective that mathematical results are used in the context of a modelling of something not necessarily mathematical, then the situation is clarified somewhat, and the procedure for arriving at justification for the use of such results becomes clear. I give an example of a particularly strong form this justification might take, using the idea of formalism independence due to Gödel and Kennedy.

   @misc{adam-day-2020-non-mathematical,
     author = {Adam-Day, Sam},
     howpublished = {Preprint},
     title = {Non-mathematical Content by Mathematical Means},
     year = {2020},
     url = {https://philarchive.org/rec/ADANCB},
   }

2019

1. 

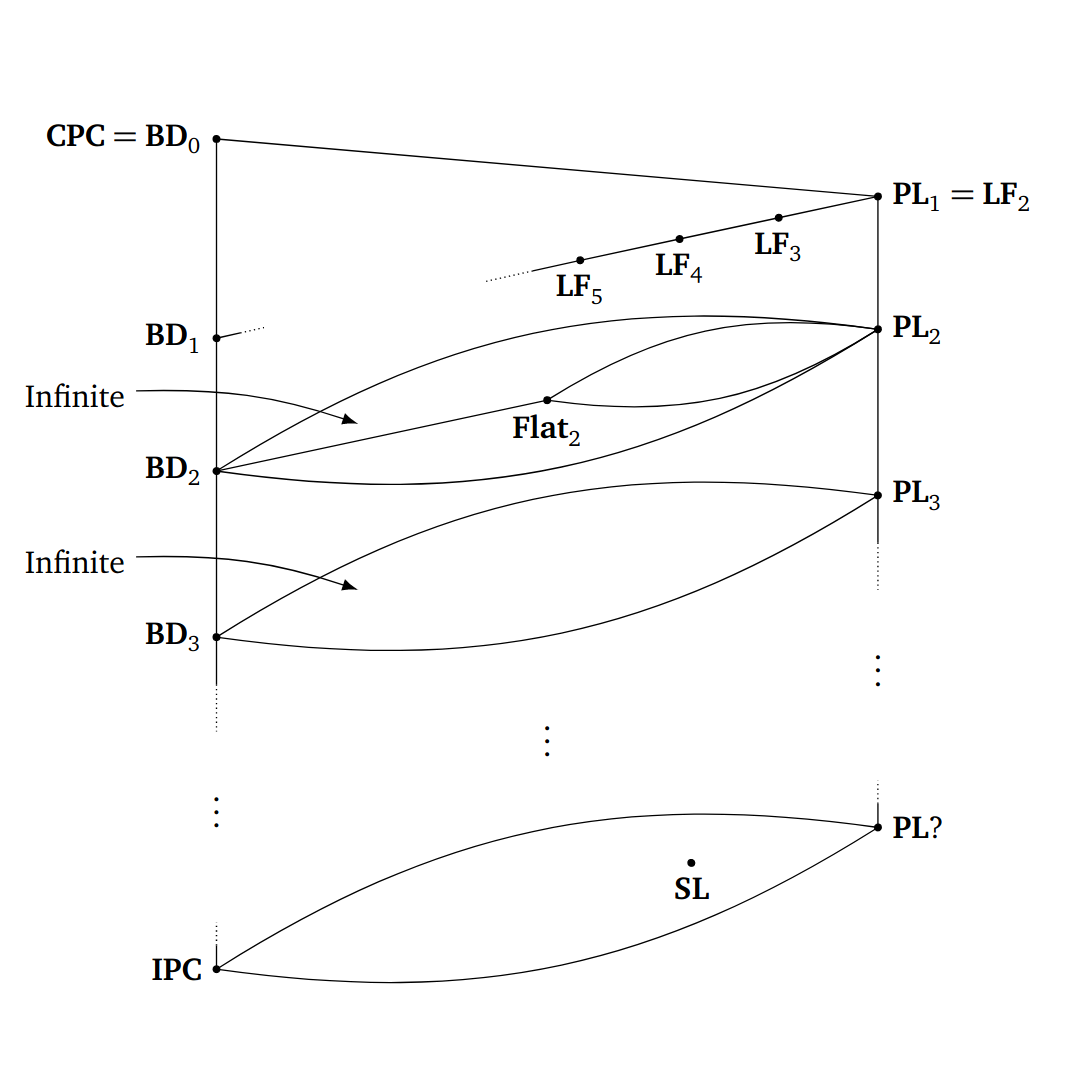   Polyhedral Completeness in Intermediate and Modal Logics

   Sam Adam-Day

   2019

   MSc Thesis

   Abs Bib PDF

   This thesis explores a newly-defined polyhedral semantics for intuitionistic and modal logics. Formulas are interpreted inside the Heyting algebra of open subpolyhedra of a polyhedron, and the modal algebra of arbitrary subpolyhedra with the topological interior operator. This semantics enjoys a Tarski-style completeness result: IPC and S4.Grz are complete with respect to the class of all polyhedra. In this thesis I explore the general phenomenon of completeness with respect to some class of polyhedra. I present a criterion for the polyhedral completeness of a logic based on Alexandrov’s nerve construction. I then use this criterion to exhibit an infinite class of polyhedrally-complete logics of each finite height, as well as demonstrating the polyhedral completeness of Scott’s logic SL. Taking a different approach, I provide an axiomatisation for the logic of all convex polyhedra of each dimension \(n\). The main conceptual contribution of this thesis is the development of a combinatorial approach to the interaction between logic and geometry via polyhedral semantics.

   @mastersthesis{adam-day-2019-msc-thesis,
     author = {Adam-Day, Sam},
     title = {Polyhedral Completeness in Intermediate and Modal Logics},
     institution = {ILLC, Universiteit van Amsterdam},
     year = {2019},
     note = {MSc Thesis},
   }